Area of Rhombus
Definition
Rhombus is a parallelogram whose all sides are equal, and its diagonals bisect each other at right angles. Now that we know what a rhombus is, we can understand what the area of rhombus signifies. Its area refers to the two-dimensional space enclosed by all the four sides of it on a 2-D plane.
Formula
For calculating the area of the rhombus, different parameters are used depending on the data available in the question. Its area generally is formulated through three cases as given below:
- When the length of the diagonals of a rhombus is given
- When its base along with the height is given
- When one of its sides and an interior angle is given
Derivation
1. When the length of the diagonals of a rhombus is given
Let ABCD be a rhombus with the length of the diagonals ‘d1’ & ‘d2’. As mentioned earlier in the definition, the diagonals of a rhombus bisect each other at right angles. In the given figure, we can see that:

∆ AOB ≅ ∆ AOD through S-S-S congruency condition as,
- DO=BO (diagonals of a rhombus bisect each other)
- AO ( Common side)
- AD=AB (sides of a rhombus are equal in length)
Similarly, it can be proved that the ∆ AOB, ∆ AOD, ∆ BCD, ∆ DOC are congruent to each other.
Area of ABCD = Area of (∆ AOB + ∆ AOD + ∆ BCD + ∆ DOC)
= 4 × area of ∆ AOB (since all the triangles are congruent, there area is equal)
= 4 × (½) × AO × OB sq. units
= 4 × (½) × (½) d1 × (½) d2 sq. units (area of a right angled triangle= ½ x base x height)
= 4 × (1/8) d1 × d2 square units
= ½ × d1 × d2
| Area = ½ × d1 × d2 |
2. When its base along with the height is given
Let ABCD be a rhombus with the length of base ‘b’ and height ‘h’. As mentioned earlier in the definition, we know that a rhombus is a parallelogram. We can use the area formula of parallelogram learnt earlier to formulate the area of the rhombus.
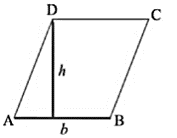
Area of a parallelogram = base x height
Since rhombus is one special kind of parallelogram, this also applies to it.
| Area of rhombus ABCD = b x h |
3. When one of its sides and an interior angle is given
Let ABCD be a rhombus with given side ‘a’ and interior angle ‘ѳ’. We know from our earlier lessons that the area of a triangle when two of its sides say ‘a’, ‘b’ and included interior angle ‘Ѳ’ is calculated as,
Area of the triangle = ½ x a x b x sin (Ѳ)
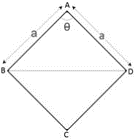
Now in the given figure, we can see that area of ABCD is the sum of areas of ΔABD & area of ΔBDC.
Area of the rhombus ABCD = area of ΔABD + area of ΔBDC
= (1/2) x a x a x Sin (Ѳ) + (1/2) x a x a x Sin (Ѳ) {area of a triangle as mentioned earlier}
= a2Sin (Ѳ)
| Area = a2Sin (Ѳ) |
Calculation Steps:
- When diagonals of the rhombus are given, half of their product gives the Area.
- When the base of the rhombus & height is given, their multiplication gives the area.
- When the angle along with a side of the Rhombus is given, the product of the square of the side & sin of the angle gives the area enclosed.
| D1 = 1/2 X D1 X D2 |
Solved Examples:
Q1- What is the area of the rhombus whose length of the sides is 4cm and height is 2cm?
|
Area = b x h |
Answer: Since the side & angle of the rhombus is given, we can use the area formula involving side & height that is:
Using this, A = 4cm x 2cm = 8cm2
| Area = a2Sin (Ѳ) |
Q2- Find the area of a rhombus whose one of the angles is 30 degrees and side is 4 cm.
Answer: With the rhombus’s angle and side given in the question, we can use the area formula,
Using this, A = 42 x Sin (30) = 8cm2
| Area = ½ × d1 × d2 |
Q3- Find the area enclosed by a rhombus with diagonals 8cm and 6cm.
Answer: Area of a rhombus with diagonals d1 & d2 is given by,
Using this, A= ½ x 8 x 6 = 24cm2
Applications:
- Automobile Industry makes use of the shape of a rhombus for designing windows.
- It finds its use in mirrors of the vehicle.
- The kites made are always in the shape of the rhombus.
Practice Multiple Choice Questions
Question:
PQRS is a rhombus. Each of its sides is 20 cm long, diagonal PR is 32 cm long and diagonal QS is 24 cm.

What is the area of PQRS?
1. 384 cm²
2. 400 cm²
3. 560 cm²
4. 768 cm²
Type your answer option :
The area of a rhombus is 40 sq cm. If one of its diagonals is 8 cm, the other diagonal is
1. 5 cm
2. 8 cm
3. 10 cm
4. 20 cm
Type your answer option :
Explore Other Topics
Related Concepts
Frequently Asked Questions
Q1. What is the perimeter of a rhombus?
Answer: The perimeter of a rhombus with side ‘a’ is the sum of all four sides of it, that is, 4a.
Q2. Are all angles of a rhombus equal?
Answer: No. Only the opposite angles of a rhombus are equal.
Q3. Do the diagonals measure the same in length in the case of a rhombus?
Answer: The diagonals of a rhombus are of different lengths in measure.
Q4. How to find the area of a rhombus when its base and height are given?
Answer: Area enclosed by four sides of a rhombus when base and height are given is base x height.
Q5. What is the area of a rhombus whose interior angle is Ѳ and side is ‘a’?
Answer: When the interior angle between two sides of a rhombus is Ѳ and side is ‘a’ then area = a2Sin (Ѳ)
Q6. In case the diagonals of a rhombus are d1 & d2, how to calculate the area enclosed in it?
Answer: If the diagonals of a rhombus are d1 & d2, Area = ½ x d1 x d2.


