AREA OF PARALLELOGRAM USING DIAGONALS

All of you must have seen Kaju katli in your life. The shape of this delicious sweet is a parallelogram. There are many other examples in our surroundings that have the shape of a parallelogram like tiles, staircases, roofs etc. This makes the role of a quadrilateral more important and conceptual knowledge becomes necessary to understand these shapes in our real life. In this article, we are going to learn about the meaning, properties, area of a parallelogram using its diagonals, derivation of formulae and some illustrations.

PARALLELOGRAM

MEANING AND PROPERTIES OF PARALLELOGRAM

A parallelogram is a 2-dimensional quadrilateral whose opposite sides and opposite angles are equal.  A rectangle is a special type of parallelogram whose interior angles are 90° and the diagonals are also equal and bisect each other. In the case of a general parallelogram, the diagonals are not equal but they bisect each other.

Some of the properties of the parallelogram are –

1. The opposite angles of a parallelogram are equal to each other.
2. The opposite sides of a parallelogram are parallel and equal.
3. The diagonals of a parallelogram bisect each other.
4. The sum of all the angles of a ∥gram is 360°.
5. The sum of the adjacent angles is 180°.
6. Either of the diagonals of a ∥gram divides it into two triangles of equal area.

AREA OF PARALLELOGRAM USING DIAGONALS

We already know that the diagonals of a parallelogram bisect each other.

The area of a parallelogram can be determined with the help of diagonals.

Formula

Area = \frac{1}{2}\times d_1\times d_2\times \sin\theta

Where d_1 = length of one diagonal, d_2 = length of other diagonal and \theta= ∠BOC between both the diagonals. The two angles that are formed are ∠BOC and ∠BOA when the diagonals intersect, we can use either of the angles because both will lead to the same result. ∠DOA and ∠DOC are equal to ∠BOC and ∠BOA respectively because they are vertically opposite angles.

DERIVATION OF AREA OF PARALLELOGRAM USING DIAGONALS

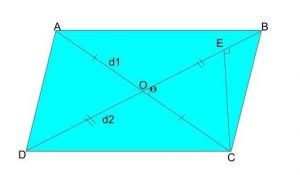
We know that either of the two diagonals of a parallelogram divides it into two congruent triangles of equal area.

So, area of ABCD = 2 × area of △BCD   – (1) (We are taking diagonal BD here)

Now, draw perpendicular CE on BD to find the area of △BCD.

Area of △BCD = ½ × CE × BD   – (2)

We can see that the △CEO is a right-angled triangle.

So, Sin𝚹 = CE/CO

⇒ CE = CO × Sin𝚹

          = Sin𝚹 × AC/2  ( AC = 2CO. Since, “diagonals of parallelogram bisect each other” )

Putting the value of CE in (2)

Area of △BCD = ½ × ½ × Sin𝚹 × AC × BD

                          = ¼  Sin𝚹 × AC × BD – (3)

Putting the value of (3) in (1)

area of ABCD = 2 × area of △BCD

                         = 2 × ¼  Sin𝚹 × AC × BD

                         = ½ × Sin𝚹 × AC × BD

                         =1/2\times d_1\times d_2\times \sin\theta \text{ } {\text{unit}}^{2}

ILLUSTRATION

Q1. Prove that either of the diagonals of a parallelogram divides it into two triangles of equal area.

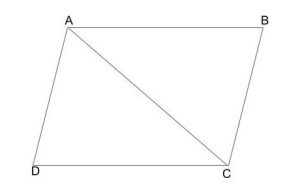
Sol.-

In parallelogram ABCD, considering diagonal AC, we get – △ADC and △ABC.

In △ADC and △CBA,

AD = BC   (opposite sides are equal to each other)

DC = AB   (opposite sides are equal to each other)

AC = AC   (Common side)

By Side Side Side (SSS) congruence rule,

△ADC ≅ △CBA

Since they are congruent, their areas are the same.

Q2. In a parallelogram ABCD, the lengths of the diagonals are 8 cm and 12 cm. The angle forming at the intersection of both the diagonals is 30°. Find the area of the parallelogram.

Sol.-

Given – d_1 = 8 cm, d_2 = 12 cm, 𝚹 = 30°

Area of parallelogram = 1/2\times d_1\times d_2\times \sin\theta

                                        = ½ × 8 × 12 × sin30°

                                        =  ½ × 8 × 12 × ½

                                        = 24 {\text{cm}}^2

Q3. Prove that the diagonals of a parallelogram divide each other into two portions of equal length.

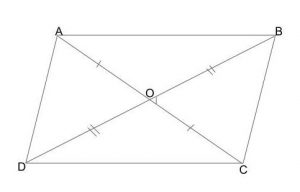
Sol.-

For proving that the diagonals bisect each other, we need to show AO = OC and DO = OB.

In △AOD and △COB,

∠OAD = ∠OCB     ( Alternate interior angles of a ∥gram )

DA = CB          ( Opposite sides are equal in a ∥gram )

∠ADO = ∠CBO     ( Alternate interior angles of a ∥gram )

By Angle side angle(ASA) congruence rule,

△AOD ≅ △COB

Thus, AO = CO & OD = OB  (Since they are corresponding parts of congruent triangles)

Hence, it is proved that the diagonals of a parallelogram divide each other into two portions

of equal length.

Q4. The height and base of a parallelogram is 16 cm and 10 cm respectively. Find the area of the parallelogram.

Sol.-

Area of parallelogram = Base (b) × Height (h)

                                        = 16 × 10

                                        = 160 {\text{cm}}^2