Area and Perimeter of a Circle with Examples and FAQs
Area and Perimeter of a Circle
The area of a circle is the total space enclosed by the circle in a 2D plane. The perimeter of the circle also known as the circumference is the total distance around and about the boundary of the circle.
Circle with O as centre and radius r
The formula for the area of the circle with radius ‘r’ is \pi r^{2}and its perimeter is 2πr. π or ‘pi’ is defined as the ratio of the circumference of a circle to its diameter. This ratio is constant. Its value is often taken to be \frac{22}{7}=3.14
Circle
A circle is a closed curve formed by a set of points that are at a fixed distance from a fixed point in the 2D plane. The fixed point is the origin or centre and the fixed distance of the points from the origin is the radius of the circle.
Different Parts of a Circle
A circle comprises of the following parts:
Perimeter: The perimeter of the circle also termed as the circumference is the total distance around and about the boundary of the circle.
Radius: Radius is the fixed distance from the centre of a circle to any point on the perimeter of the circle. A circle has an infinite number of radii as it is the distance from the centre and it can touch the perimeter at various points and in various manners.
Diameter: A diameter is a straight line that passes through the centre and it connects two points on the perimeter of the circle. There can be multiple diameters in the circle, but they should follow these rules:
- The diameter always passes through the centre.
- It should be a straight line.
- It should touch the boundary of the circle at two points.
- Its value is twice that of the radius of the circle.
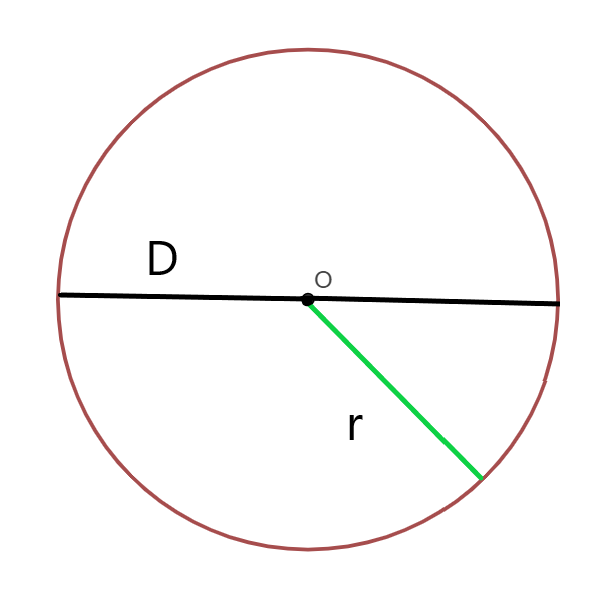
The figure represents a circle with O as centre and ‘r’ as its radius. ‘D’ represents the diameter.
The Perimeter of a Circle
The perimeter of a closed figure is the measurement of its boundary length. If the circle is opened to form a straight line then the length of this line is the circumference. The perimeter of a circle with ‘r’ as the radius is:
Perimeter = 2πr units
Note: π, ‘pi’ is defined as the ratio of the circumference of a circle to its diameter. This ratio, i.e., pi has a constant value. Let a circle have radius ‘r’ and circumference ‘C’. Then for this circle
π = Circumference/Diameter
⇒ π = C/2r [ as the diameter of a circle is 2r]
⇒ C = 2πr
Area of a Circle
The area of a circle is the total space enclosed by the circle in a 2D plane. If a circle has a radius ‘r’ then the area of the circle = \pi r^{2} square units, where π = \frac{22}{7} or 3.14
Area of a circle =\pi r^{2} square units
Area of a circle can be calculated by using different formulas which are:
Area when the radius is known:
Area =\pi \times r^{2} square units, where ‘r’ is the radius.
Area when the diameter is known:
Area = (\pi / 4) \times D^{2} square units, where ‘D’ is the diameter.
Area when perimeter(circumference) is known:
Area =\mathbf{P}^{2} / 4 \pi square units, where ‘P’ is the perimeter.
Examples
Example 1: If the radius of a circle is 14 cm. Then find its perimeter and area.
Solution:
The given measurement of the radius of the circle is 14 cm.
∴ Perimeter =2 \pi r=2 \times \frac{22}{7} \times 14=88 \mathrm{~cm}
And Area =\pi r^{2}=\frac{22}{7} \times 14 \times 14 \mathrm{~cm}^{2}=616 \mathrm{~cm}^{2}
Hence, the perimeter is 88 cm and the area is616 \mathrm{~cm}^{2}
Example 2: The circumference of the circle is 66 cm. Find the area of the circle.
Solution:
It is given that the circumference of a circle is 66 cm.
\Rightarrow 2 \pi r=66 \mathrm{~cm}
\therefore r=\frac{66}{2 \pi}=\frac{66 \times 7}{2 \times 22} \mathrm{~cm}=10.5 \mathrm{~cm}
Therefore, area =\pi r^{2}=\frac{22}{7} \times 10.5 \times 10.5 \mathrm{~cm}^{2}
=346.5 \mathrm{~cm}^{2}
Explore Other Topics
Related Concepts
Frequently Asked Questions
1. What is the area of a circle?
Ans: The area of a circle whose radius is ‘r’ is \pi r^{2}
2. What is the perimeter of a circle?
Ans: The perimeter of the circle also known as the circumference is equal to 2πr.
3. How to determine the area of the circle if the diameter is known?
Ans: The diameter of a circle is two times the radius of the circle, i.e., diameter= 2 × radius.
Hence radius of a circle if its diameter is ‘D’ is D/2.
\therefore \text { Area }=\pi\left(\frac{D}{2}\right)^{2}=\frac{\pi D^{2}}{4}
