Area of a semicircle – Mindspark

Area of a semicircle

A semi-circle is half a circle. When a straight line is drawn through a circle in such a manner that the line passes through the centre of the circle, then such a line would cut the circle into exactly two equal halves, and each half is a semicircle. A common example of a semicircle is the protractor in our geometry box. 

Let us try to understand how to calculate the area of a semicircle in this article. 

Formula:

The area of a semicircle is the number of square units that can be filled within a semicircle.  A semicircle is half of a circle. Hence, the area of a semicircle is half the area of a circle. 

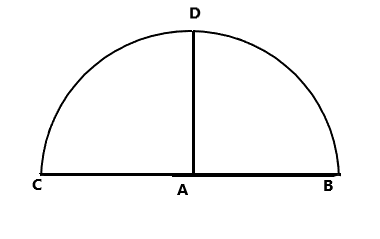
The radius in the above semicircle is the distance between any point on the arc BDC and the midpoint A.

Hence, AC = AB = AD = Radius.

We know that the area of a circle with radius  ‘r’ is \left(\pi \times r^{2}\right) \text { unit }^{2}.

Since a semicircle is a half circle,

The area of a semicircle with a radius ‘r’ is \left(\frac{1}{2} \times \pi \times r^{2}\right)\text { unit }^{2}and \pi is constant at 3.14 or \frac{22}{7} 

Examples:

• Find the area of a semicircle where the diameter of the semicircle is 18 cm?

Solution:

the area of a semicircle is \frac{1}{2} \times \pi \times r^{2} \text { unit }^{2}. In the given question, r = 9 cm

Substituting the value of r = 9 cm in the formula,

Area of semicircle = =\frac{1}{2} \times \frac{22}{7} \times 9^{2} \mathrm{~cm}^{2}

                                     =127.29 \mathrm{~cm}^{2}

2. Mr.C buys a circular clock where the length of the minute hand is 21 cm. Calculate the area covered by the minute hand in 30 minutes.

Solution:

It is given that the length of the minute hand is 21 cm. This is the radius of the circular clock. So, to calculate the area covered by the minute hand in 30 minutes, we have to calculate the area of the semicircle.

The area of a semicircle is \frac{1}{2} \times \pi \times r^{2} \text { unit }^{2}, where r = radius.

Using the value of r = 21 cm in the formula,

Area of semicircle = \frac{1}{2} \times \frac{22}{7} \times 21^{2} \mathrm{~cm}^{2}

                                  =693 \mathrm{~cm}^{2}

3. Mr. X and Mr. Y are hired to clean a circular park. The distance from the middle of the park to any point on the park’s boundary is 350 meters. Mr. X and Mr. Y each agree to clean exactly half the park. Calculate the area of the park cleaned by Mr.X.

Solution:  It is given that the distance between the centre to any point on the park’s boundary is 350 m. This is the radius of the park. Since Mr. X is cleaning only half of the park, we have to calculate the area of the semicircle.

The area of a semicircle is \frac{1}{2} \times \pi \times 1^{2} \text { unit }^{2}, where r = radius.

Substituting the value of r = 350 m in the formula,

Area of semicircle =\frac{1}{2} \times \frac{22}{7} \times 350^{2} \mathrm{~m}^{2}

                                   =1,92,500 \mathrm{~m}^{2}