Lateral Surface Area with Examples and FAQs
LATERAL SURFACE AREA
The lateral surface area is the area of any solid which gives the area occupied by its sides, it excludes the top and bottom bases. It is also termed as the curved surface area for cylindrical, spherical and conical objects, which is the area of the curved surface or the sides of the three-dimensional figures. The methods to find out the lateral surface area of solid figures like cube, cuboid, cone, sphere, hemisphere, cylinder, etc., are all different but can be easily determined if the basic dimensions of important parts are known.
FORMULA FOR LATERAL SURFACE AREA OF DIFFERENT SOLIDS
1.Cube
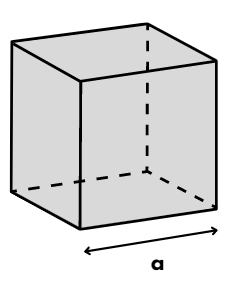
The Lateral Surface area of a cube with side length “a” = 4 a^{2}
2. Cuboid

The Length of a cuboid is ‘l’ its breadth is ‘b’ and its height is ‘h’
The lateral surface area of the cuboid =2(l+b) h
3. Cylinder

The radius of the base cylinder of the cylinder is ‘r’ and its height is ‘h’
The lateral surface area of cylinder =2 \pi \mathrm{rh}
4. Cone

The radius of the base of the cone is ‘r’, the cone’s height is ‘h’
The slant height l=\sqrt{h^{2}+r^{2}}
The Lateral Surface Area of Cone =\pi \mathrm{rl}
5. Sphere

The Radius of Sphere is ‘r’
The Lateral Surface Area of Sphere =4 \pi \mathrm{r}^{2}
6. Hemisphere

The Radius of the hemisphere is ‘r’
The Lateral Surface Area of Hemisphere =2 \pi \mathrm{r}^{2}
Examples
Example 1: The diameter of the base and height of a cylinder is 14 units and 20 units respectively. Calculate the lateral surface area.
use\pi=\frac{22}{7}
Solution:
Diameter of the base of the cylinder = 14 units
⇒ radius, r =14/2 units =7 units
Height of cylinder, h = 20 units
Lateral area of the cylinder
=2 \pi \mathrm{rh}
=2 \times \frac{22}{7} \times 7 \times 20
=2 \times 22 \times 20 \text { square units }
=880 \text { square units }
Hence, the lateral surface area of the given cylinder is 880 square units.
Example 2 :
The radius of a cone measures 5 cm and its height is 12 cm. Determine the LSA of the cone. [use value of π =3.14]
Solution:
Radius of the cone r = 5cm
Height of the cone h = 12cm
Slant height l=\sqrt{r^{2}+h^{2}}
\therefore \mathrm{l}=\sqrt{5^{2}+12^{2}}=\sqrt{25+144}=\sqrt{169}=13 \mathrm{~cm}
Hence Lateral Surface area of cone =\pi \mathrm{rl}
=3.14 \times 5 \times 13 \mathrm{~cm}^{2}
= 204.1 {~cm}^{2}
Therefore, the LSA of the cone is 204.1 {~cm}^{2}
Example 3: Find the lateral area of a cuboid whose length is 12 units, breadth is 8 units and height is 5 units.
Solution:
Length of cuboid, l = 12 units.
Breadth of cuboid, b = 8 units.
Height of cuboid, h = 5 units.
Therefore Lateral Area of a cuboid
=2 \times(1+b) \times h
=2 \times(12+8) \times 5 Square units
=2 \times 20 \times 5 Square units
Therefore, the lateral area of the given cuboid is 200 square units.
Explore Other Topics
Related Concepts
Frequently Asked Questions
1. How is the Lateral Surface Area of a Cone determined?
Ans: The LSA of a cone = πrl.
Where r is the radius, l is its slant height and π (pi) is a constant term with a value of 3.14 or \frac{22}{7}.
2. What Is the Lateral Surface Area of a Cylinder?
Ans: The LSA of a cylinder = 2πrh.
Where r is the radius, h is its height and π (pi) is a constant term with a value of 3.14 or \frac{22}{7}.
3. What are the LSA of a Cube and a Cuboid?
Ans: The LSA of a Cube =4 \mathrm{p}^{2}
Where ‘p’ is the length of the edge of the square.
The LSA of a Cuboid = 2 ✕(L + B ) ✕ H.
Where ‘L’ is the length, ‘B’ is the breadth and ‘H’ is the height of the cuboid.
4. What are the LSA of a sphere and a hemisphere?
Ans: The LSA of a sphere =4 \pi \mathrm{r}^{2}
Where r is the radius of the sphere and π (pi) is a constant term with a value of 3.14 or \frac{22}{7}.
Hemisphere is half of the sphere hence the LSA will also be half that of the sphere.
The LSA of a hemisphere =2 \pi \mathrm{r}^{2}
Where r is the radius of the hemisphere and π (pi) is a constant term with a value of 3.14 or \frac{22}{7}.
