Solid Shapes with Examples and FAQs

What are solid shapes?

The shapes the are 3 dimensional and occupy matter(space) are known as solid shapes. The three dimensions are length, breadth and height or depth of the object.

The following are some solid shapes that are a part of our day to day life:

Types of Solids and their Specific Characteristics

1. Cube

Characteristics of a Cube:

• A cube comprises 6 square faces, 12 edges and 8 vertices.
• If the edge length is ‘a’ units, then:

          Lateral Surface Area(LSA) =4 a^{2}

          Total Surface Area(TSA) =6 a^{2}       

          Volume =a^{3}

2. Cuboid

Characteristics of a cuboid:

• A cuboid comprises 6 rectangular faces, 12 edges and 8 vertices.
• If the length, breadth and height of a cuboid is l, b and h units respectively then:

           Lateral Surface Area(LSA) = 2(l + b)h

           Total Surface Area(TSA) = 2(lb + bh + lh)

           Volume = lbh

3. Cylinder

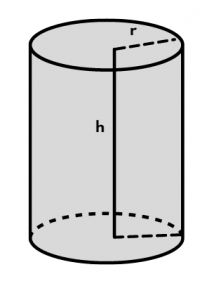
Characteristics of a cylinder:

• Comprises of two circular planes as bases and one curved surface.
• It also has 2 edges and no vertices.
• If the height of a cylinder is ‘h’ units and the radius of its circular bases if ‘r’ units, then:

          Curved Surface Area(CSA) = 2πrh

          Total Surface Area(TSA) = 2πr(r + h)

          Volume =\pi r^{2} h

4. Cone

Characteristics of a cone:

• Comprises of 2 faces: 1 circular plane as the base and 1 curved surface, one edge and one vertex.
• If the height of a cone is ‘h’ units, slant height is ‘l’ units and radius of the circular base is ‘r’ units, then:

          Curved Surface Area(CSA) = πrl

          Total Surface Area(TSA) =πr(r+l)

          Volume =\frac{1}{3} \pi r^{2} h

5. Sphere

Characteristics of a sphere:

• Comprises of 1 curved surface(face), no edge and no vertex.
• Each point on a sphere is equidistant from its centre and i.e., its radius, if this radius is ‘r’ units, then:

          Total Surface Area(TSA) =4 \pi r^{2}        

          Volume =\frac{4}{3} \pi r^{3}

6. Hemisphere

Characteristics of a hemisphere:

• Comprises of 1 circular plane as a surface(face) and 1 flat circular face, 1 edge and no vertex.
• Each point on a hemisphere is equidistant from its centre and i.e., its radius, if this radius is ‘r’ units, then:

         Curved Surface Area(CSA) =2 \pi r^{2}

         Total Surface Area(TSA)=3 \pi r^{2}

         Volume=\frac{2}{3} \pi r^{3}

Examples

Identify the solids.

a.

b.

c.

Solution:

The solids are:

a. Box- Cube

b. Ice Cream- Cone

c. Building- Cuboid